As I’m self studying algorithms and data structures with python from here, I figured I could try to do some experiments with different sorting algorithms using my own implementations in R.

Types of sorting algorithms I will use:

Bubble Sort
Insertion Sort
Selection Sort
Shell Sort
Merge Sort
Quick Sort

I will be dealing with a vector of type double. It can be a collection of any real positive numbers.

set.seed(3706)

The following function is used as a sanity check to confirm that each function sorts the given vector as it should.

check_works_correct <- function(myFunc){
  tmp <- function(myfunc) {
    x <- sample(100, 50) # integers; This checks that the algorithm works as it should even with duplicates
    y <- runif(50, 0, 500)
    return(identical(sort(x), myfunc(x)) && identical(sort(y), myfunc(y))) # compare to R's sort function
  }
  return(all(replicate(n = 100, tmp(myFunc))))
}

Write Sorting Algorithms

Bubble Sort

bubble_sort <- function(x) {
  pass_remain <- length(x)
  swapped <- TRUE
  while ((pass_remain >= 1) & swapped) {
    swapped <- FALSE
    a <- 1
    b <- 2
    while (a < pass_remain) {
      if (x[a] > x[b]) {
        tmp <- x[a]
        x[a] <- x[b]
        x[b] <- tmp
        swapped <- TRUE
      }
      a <- a + 1
      b <- b + 1
    }
    pass_remain <- pass_remain - 1
  }
  return(x)
}

check_works_correct(bubble_sort)

## [1] TRUE

Insertion Sort

insertion_sort <- function(x) {
  for (i in 2:length(x)) {
    item <- x[i]
    pos <- i
    while ((x[pos - 1] > item) && (pos > 1)) {
      x[pos] <- x[pos - 1]
      pos <- pos - 1
    }
    x[pos] <- item
  }
  return(x)
}

check_works_correct(insertion_sort)

## [1] TRUE

Selection Sort

selection_sort <- function(x) {
  for (i in seq(length(x), 1, -1)) {
    max_ind <- 1
    for (j in 1:i) {
      if (x[j] > x[max_ind]) {
        max_ind <- j
      }
    }
    tmp <- x[i]
    x[i] <- x[max_ind]
    x[max_ind] <- tmp
  }
  return(x)
}

check_works_correct(selection_sort)

## [1] TRUE

Shell Sort

shell_sort <- function(x) {
  # choose max increment (Hibbard Increment)
  k <- floor(log(length(x)+1, 2))
  # sort all the sublists with the increment, while decreasing the increment
  while (k > 0) {
    gap <- 2^k - 1
    # sort each sublist with insertion sort
    for (i in 1:gap) {
      compare_pos <- i + gap
      while (compare_pos < (length(x) + 1)) {
        item <- x[compare_pos]
        pos <- compare_pos
        while (x[pos-gap] > item && pos > i) {
          x[pos] <- x[pos-gap]
          pos <- pos-gap
        }
        x[pos] <- item
        compare_pos <- compare_pos + gap
      }
    }
    # decrement
    k <- k - 1
  }
  return(x)
}

check_works_correct(shell_sort)

## [1] TRUE

Merge Sort

# merge sort with recursion
merge_sort <- function(x) {
  if (length(x) < 2) { # base case
    return(x)
  } else {
    break_point <- length(x) %/% 2
    
    # break the vector into two
    left <- x[1:break_point]
    right <- x[(break_point+1):length(x)]
    
    # recurecurecursionsionsion
    left <- merge_sort(left)
    right <- merge_sort(right)
    
    insert_pos <- 1
    left_pos <- 1
    right_pos <- 1
    
    # merge left and right
    while (left_pos <= length(left) && right_pos <= length(right)) {
      if (left[left_pos] <= right[right_pos]) {
        x[insert_pos] <- left[left_pos]
        left_pos <- left_pos + 1
      } else {
        x[insert_pos] <- right[right_pos]
        right_pos <- right_pos + 1
      }
      insert_pos <- insert_pos + 1
    }
    
    if (left_pos <= length(left)) {
      while (left_pos <= length(left)) {
        x[insert_pos] <- left[left_pos]
        left_pos <- left_pos + 1
        insert_pos <- insert_pos + 1
      }
    }
    
    if (right_pos <= length(right)) {
      while (right_pos <= length(right)) {
        x[insert_pos] <- right[right_pos]
        right_pos <- right_pos + 1
        insert_pos <- insert_pos + 1
      }
    }
    
    return(x)
  }
}
check_works_correct(merge_sort)

## [1] TRUE

Quick Sort

quick_sort <- function(x) {
  low <- 1
  high <- length(x)
  x <- quick_sort_helper(x, low, high)
  return(x)
}

quick_sort_helper <- function(x, low, high) {
  if (low >= high) {
    return(x)
  } else {
    # choose pivot
    mid <- (low + high) %/% 2
    if ((x[low] < x[mid] && x[mid] < x[high]) || (x[high] < x[mid] && x[mid] < x[low])) {
      median_ind <- mid
    } else if ((x[mid] < x[low] && x[low] < x[high]) || (x[high] < x[low] && x[low] < x[mid])) {
      median_ind <- low
    } else {
      median_ind <- high
    }
    
    # put pivot to last index
    pivot <- x[median_ind]
    if (median_ind != high) {
      x[median_ind] <- x[high]
      x[high] <- pivot
    } 
    
    left <- low
    right <- high-1
    
    # rearrange the values around the pivot
    done <- FALSE
    while (!done) {
      while (left <= right && x[left] < pivot) {
        left <- left + 1
      }
      while (right >= left && x[right] >= pivot) {
        right <- right - 1
      }
      if (left > right) {
        done <- TRUE
      } else {
        tmp <- x[right]
        x[right] <- x[left]
        x[left] <- tmp
      }
    }
    x[high] <- x[left]
    x[left] <- pivot
    
    x <- quick_sort_helper(x, low, left-1)
    x <- quick_sort_helper(x, left+1, high)
  }
  return(x)
}

check_works_correct(quick_sort)

## [1] TRUE

Now I’ll compare the runtime of each sort, varying the size and shape of the graphs.

Generate Unordered Sequences with Varying Trends

I built the function generate_random_sequence, which accepts the following to generate a random sequence:

trend: a function that describes the general trend of the sequence of the sequences
n: number of points
low: lowest x value. Defaults to 0.
high: highest x value. Defaults to 10.
noise: a function to be used to generate noise for the sequence. Defaults to a Gaussian Distribution with mean 0 and sd 5

generate_random_sequence <- function(trend, n, low=0, high=10, noise = function(x) rnorm(x, 0, 5)) {
  # trend: a function; general trend of the sequence
  # noise: a function; amount of noise you want to add to a sequence
  x <- trend(seq(low, high, length.out = n)) + noise(n)
  if (any(x <= 0)) {
    x <- x + abs(min(x)) + 1
  }
  return(x)
}

For example, suppose I want to generate a sequence of length n = 100 that follows a quadratic trend. (I put less emphasis on the aesthetics of the graphs. I just wanted to quickly demonstrate the graphs.)

trend1 <- function(x) (x-5)^2 # quadratic trend
x1 <- generate_random_sequence(trend1, 100)

par(mfrow = c(1, 2), mar = c(1, 0.1, 2, 2), oma=c(1.5,2,2,1))
plot(x1, xaxt = 'n', main = 'Scatterplot', xlab='')
barplot(x1, main = 'Barplot')
mtext(expression(bold("Sequence with Quadratic Trend")), outer=TRUE, cex=1.5)

Create various types of trends

quadratic_trend <- function(x) (x-5)^2
right_skew_trend <- function(x) dgamma(x, 4, 2) * 10
left_skew_trend <- function(x) dgamma(10-x, 4, 2) * 10
symmetrical_trend <- function(x) dnorm(x, 5, 1.3) * 10
flat_trend <- function(x) dunif(x, 0, 10) * 10
sine_trend <- function(x) sin(x*2) * 5 

trend_list <- list(
  # all range from 0 to 10
  quadratic_trend = quadratic_trend,
  right_skew_trend = right_skew_trend, 
  left_skew_trend = left_skew_trend, 
  symmetrical_trend = symmetrical_trend, 
  flat_trend = flat_trend, 
  sine_trend = sine_trend
)

par(mfrow = c(1, 2))
for (i in 1:length(trend_list)) {
  plot(trend_list[[i]], 0, 10, main = names(trend_list)[i], xaxt = "n", xlab = "")
}

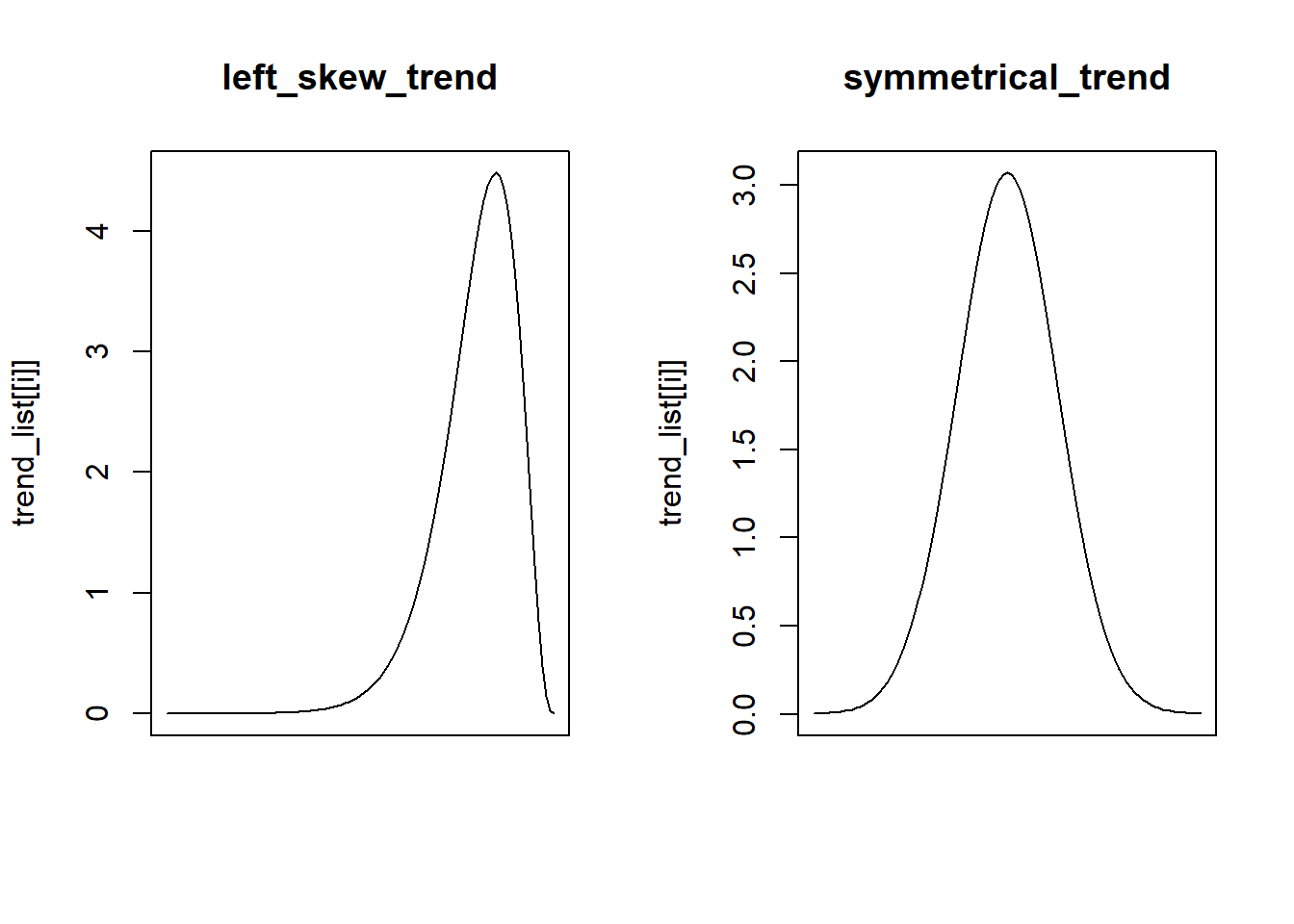
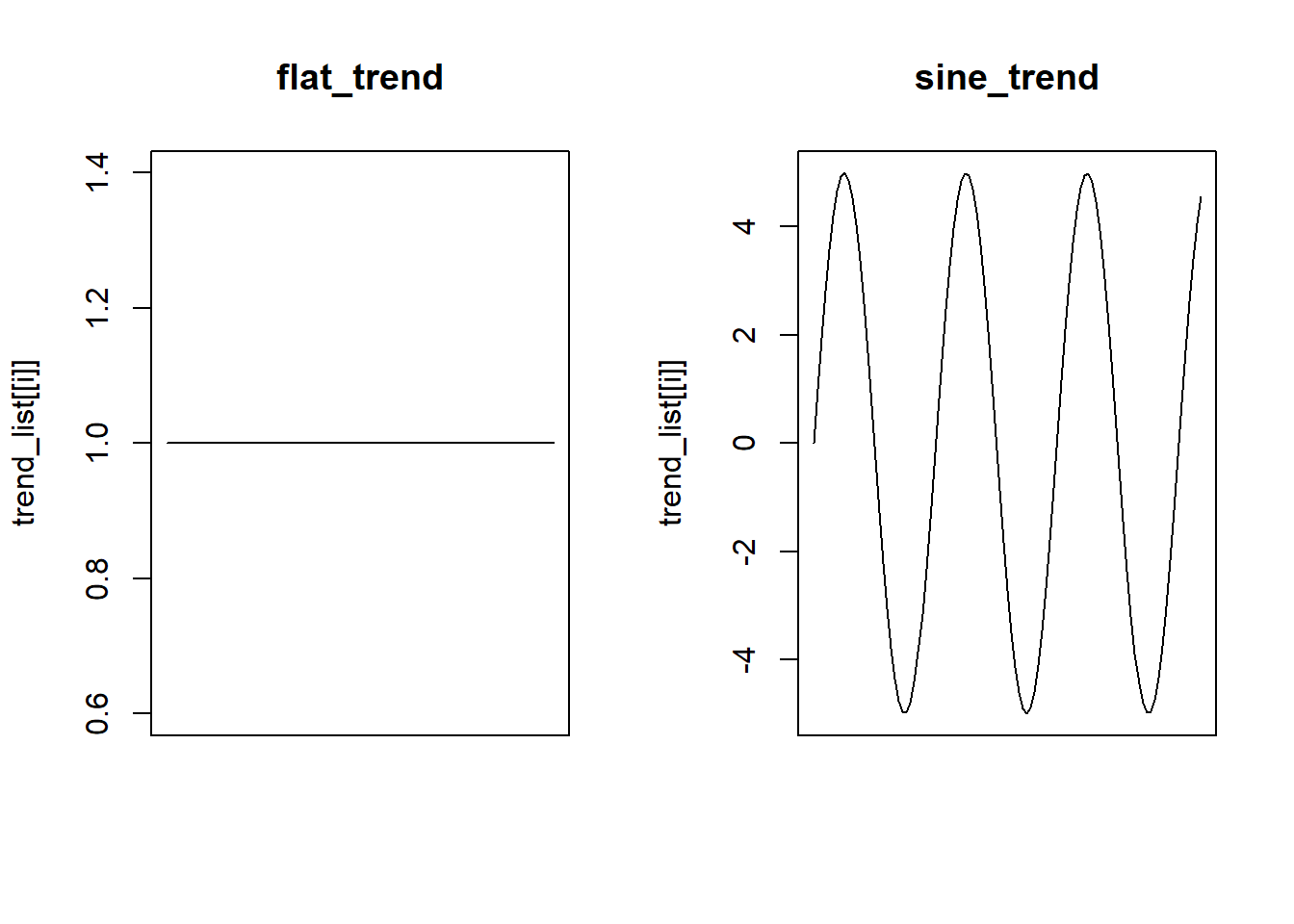
What they look like when noise is added:

par(mfrow = c(1,2))
barplot(generate_random_sequence(quadratic_trend, 100, noise = function(x) rnorm(x, 0, 5)), main = "Quadratic Trend")
barplot(generate_random_sequence(right_skew_trend, 100, noise = function(x) rnorm(x, 0, 1)), main = "Right Skew Trend")
barplot(generate_random_sequence(left_skew_trend, 100, noise = function(x) rnorm(x, 0, 1)), main = "Left Skew Trend")
barplot(generate_random_sequence(symmetrical_trend, 100, noise = function(x) rnorm(x, 0, 0.7)), main = "Symmetrical Trend")
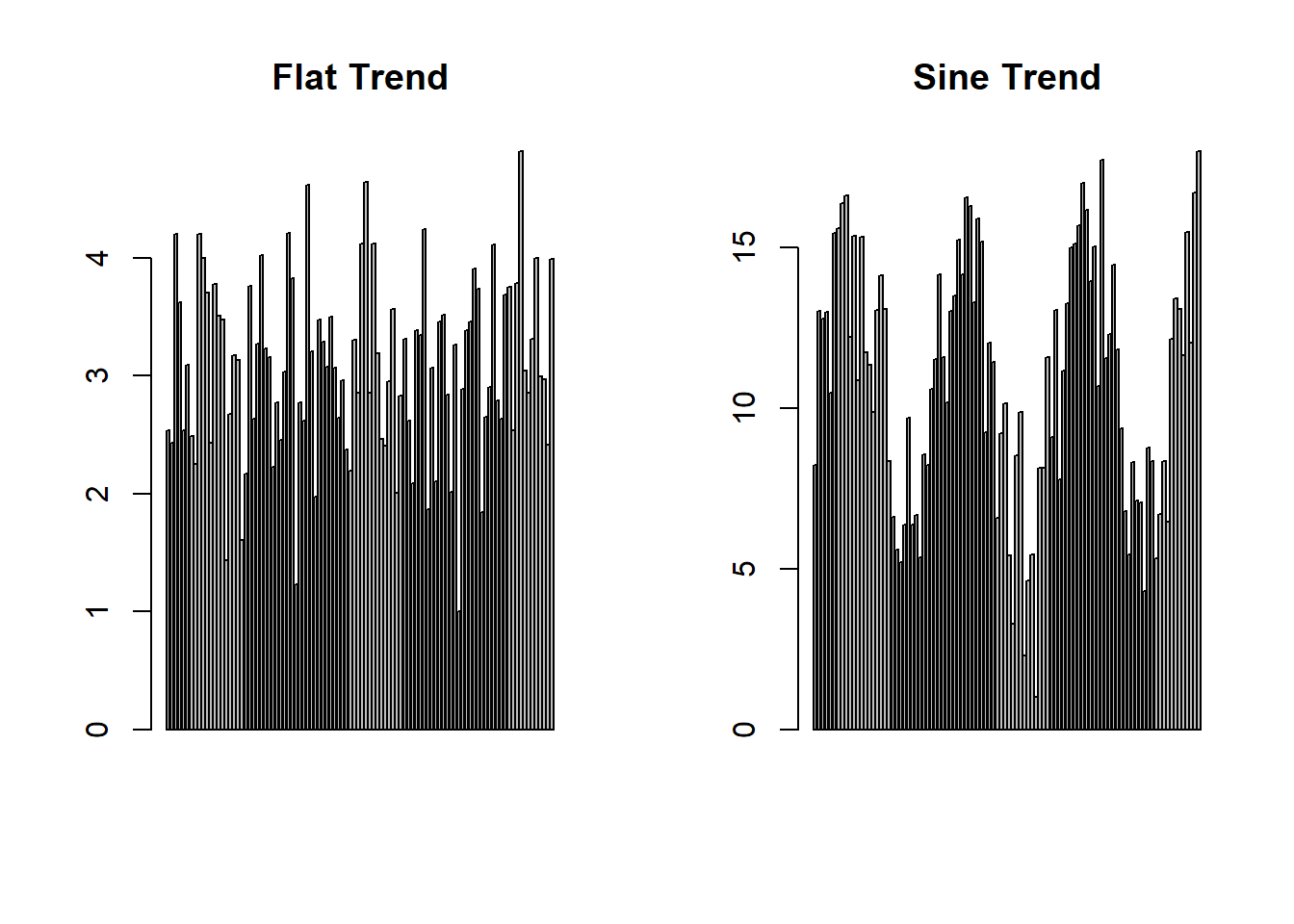
barplot(generate_random_sequence(flat_trend, 100, noise = function(x) rnorm(x, 0, 0.8)), main = "Flat Trend")
barplot(generate_random_sequence(sine_trend, 100, noise = function(x) rnorm(x, 0, 2)), main = "Sine Trend")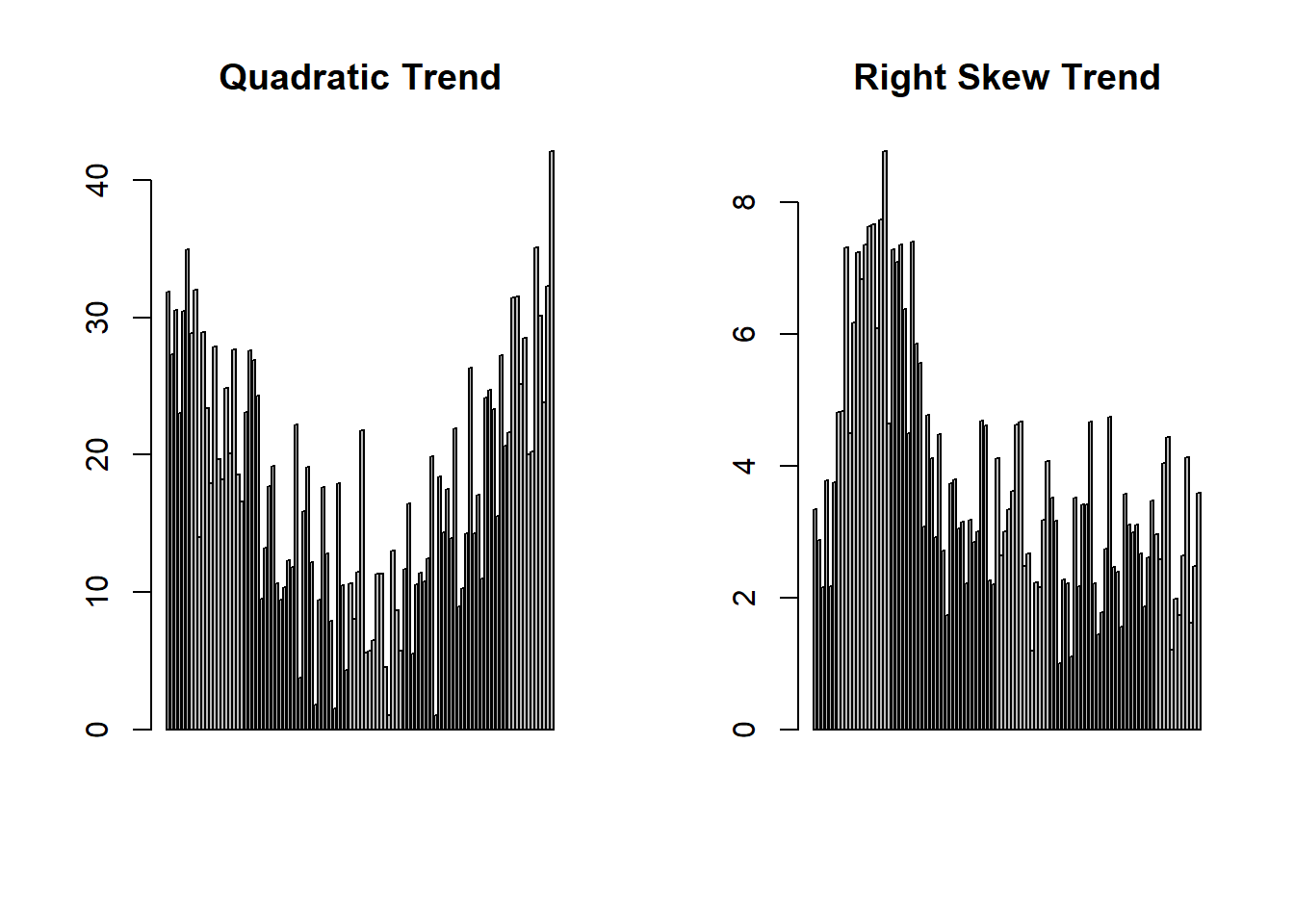

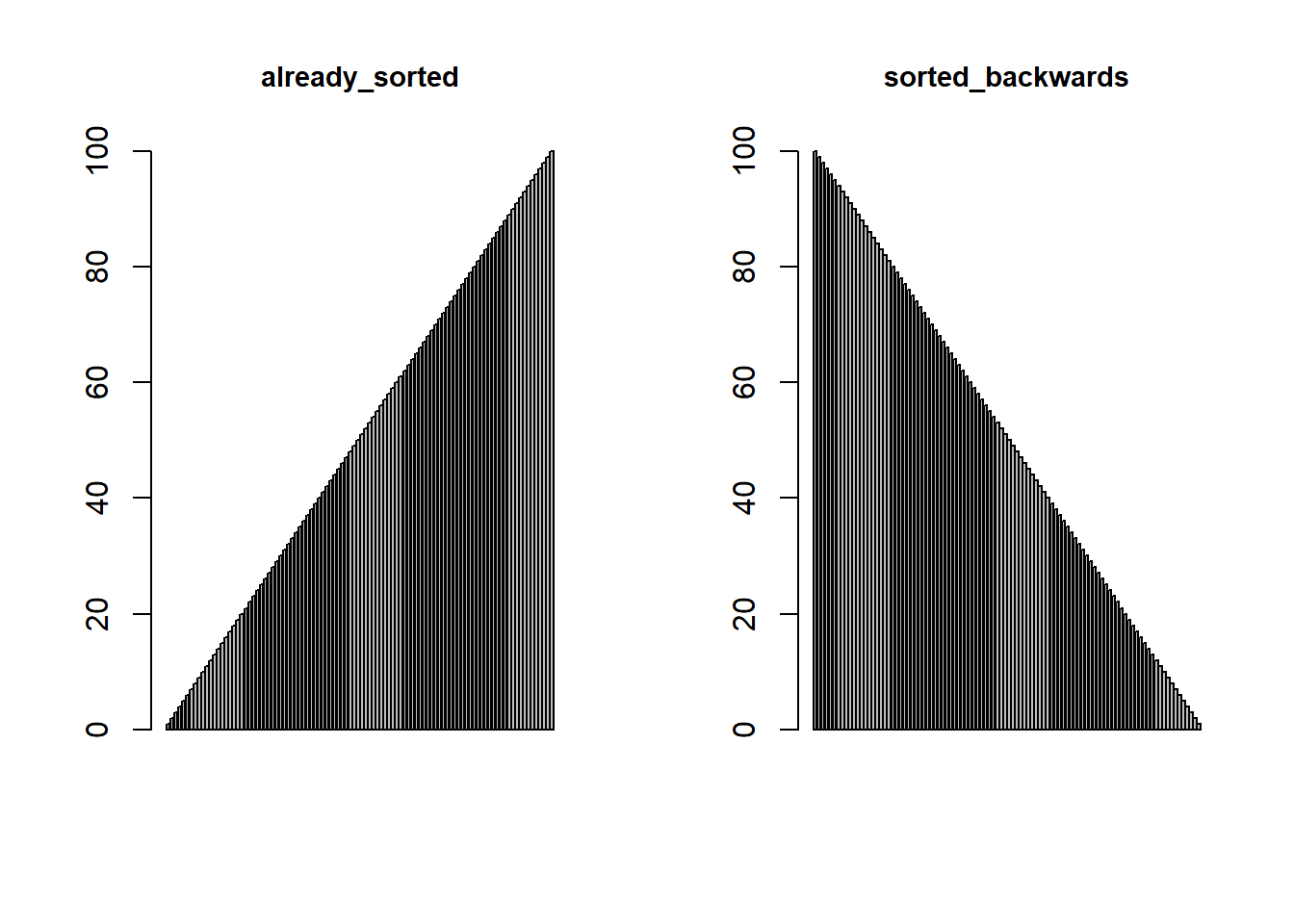
Also, consider some special cases, such as already sorted, sorted backwards, etc.

already_sorted <- function(n) seq(1, n)
sorted_backwards <- function(n) seq(n, 1, -1)
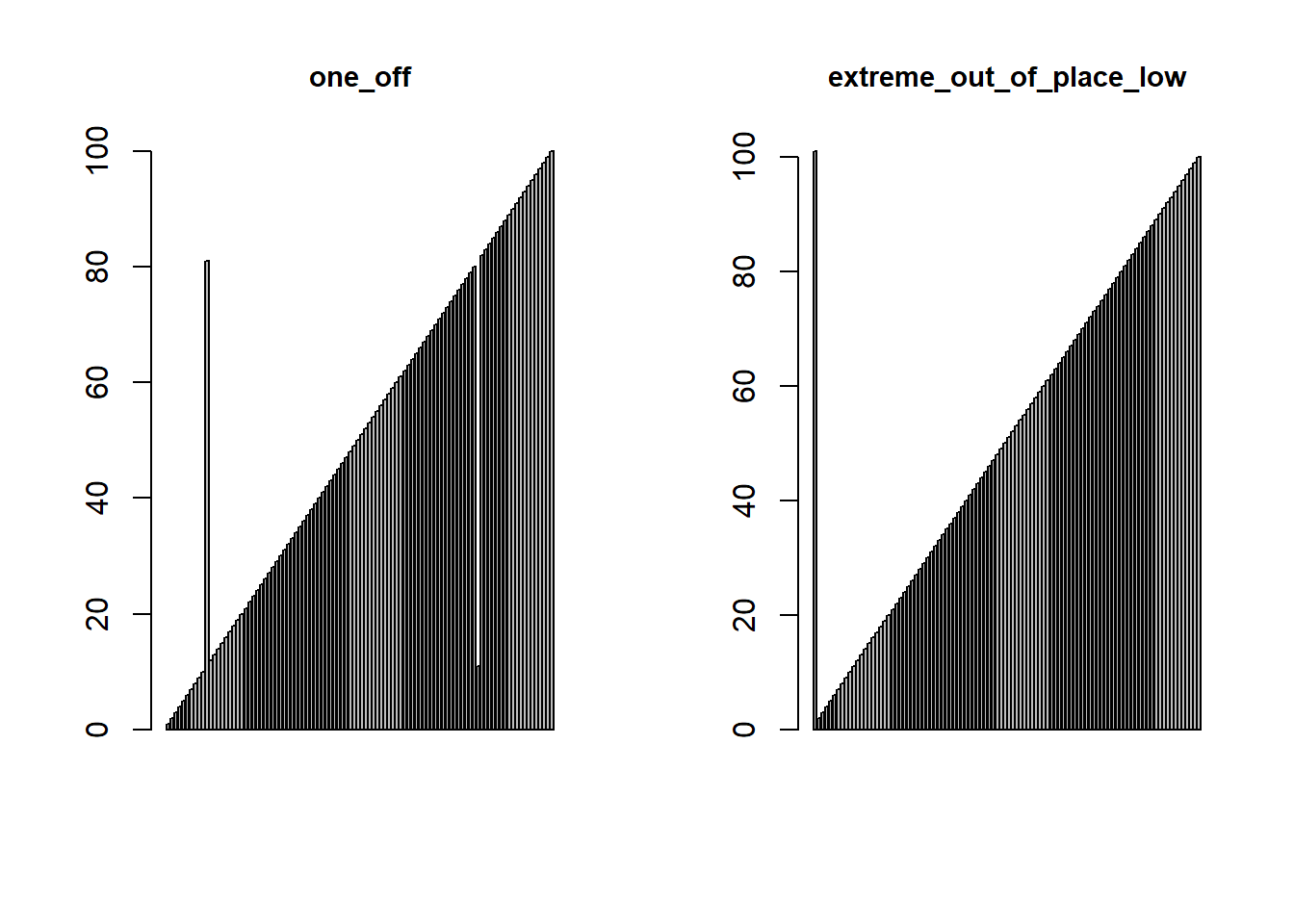
one_off <- function(n) {
  mySeq <- seq(1, n)
  random_index <- sample(mySeq, 2)
  mySeq[random_index] <- mySeq[random_index[c(2,1)]]
  return(mySeq)
}
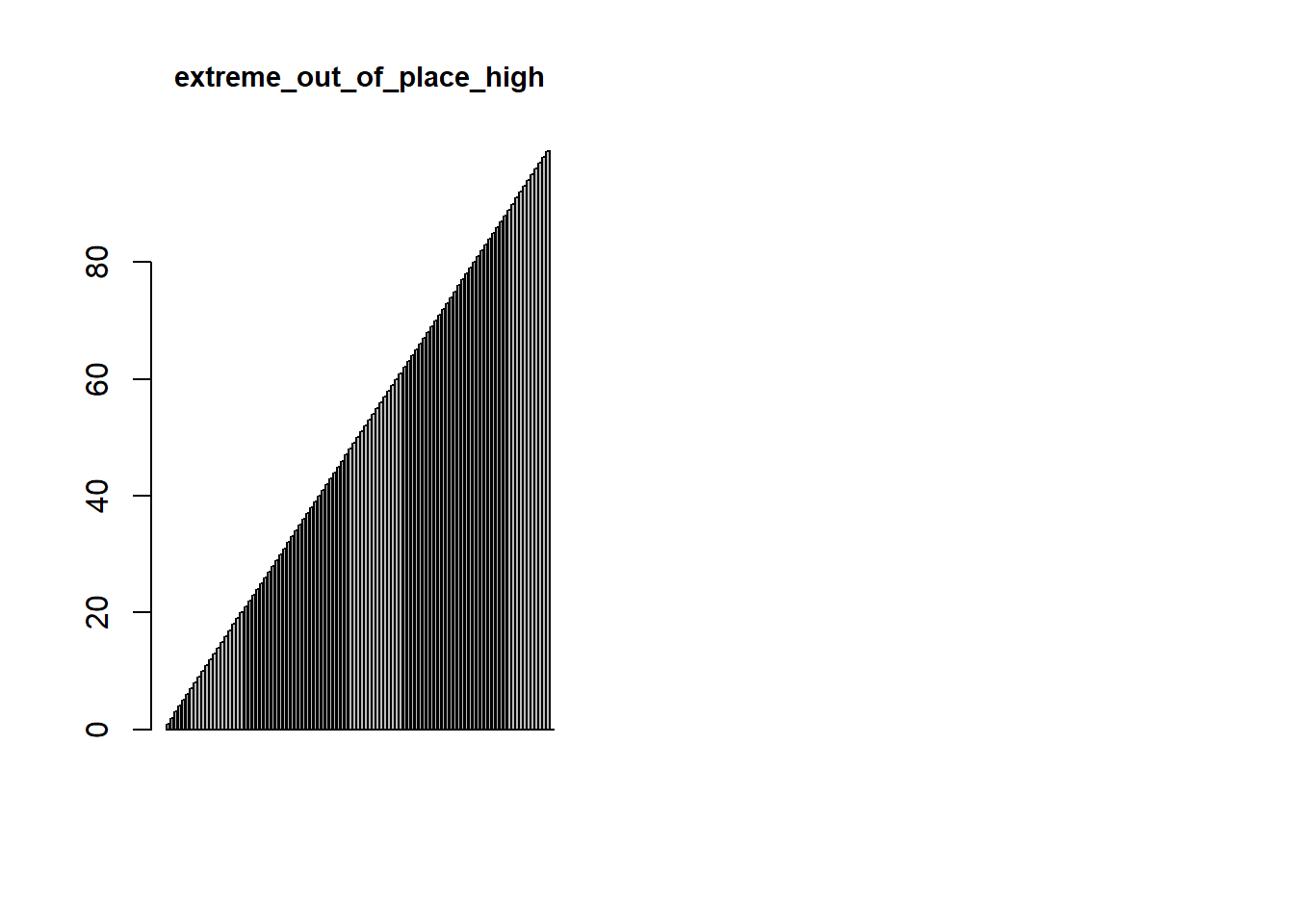
extreme_out_of_place <- function(n, lowest=TRUE) {
  mySeq <- seq(1,n)
  index <- ifelse(lowest, 1, length(mySeq))
  replace_val <- ifelse(lowest, n+1, 0)
  mySeq[index] <- replace_val
  return(mySeq)
}

special_case_list <- list(
  already_sorted = already_sorted,
  sorted_backwards = sorted_backwards,
  one_off = one_off,
  extreme_out_of_place_low = function(x) extreme_out_of_place(x, TRUE),
  extreme_out_of_place_high = function(x) extreme_out_of_place(x, FALSE)
)

par(mfrow = c(1,2))
for (i in 1:length(special_case_list)) {
  barplot(special_case_list[[i]](100), main = names(special_case_list)[i], cex.main = 0.9)
}

Sorting with Different Algorithms

Now that I have the tools to construct random sequences, I can finally start generating sequences and run benchmarks.

For future convenience, I saved the results in two different lists: trend_sort_time and special_case_sort_time. Each list are divided by number of unsorted sequences (10, 100, 1000). And for each number are microbenchmarks for each “trends” or “special cases”.

microbenchmark is used to precisely evaluate the performance of each algorithm. Each sorting algorithm sorts randomly generated data 100 times. On each iteration, sequences are randomly generated, and each algorithm sorts the same sequence.

Microbenchmark for trends:

library(microbenchmark)

## Warning: package 'microbenchmark' was built under R version 4.0.5

# each trend uses different noise scale.
noise_list <- list(
  "quadratic_trend" = function(x) rnorm(x, 0, 5),
  "right_skew_trend" = function(x) rnorm(x, 0, 1),
  "left_skew_trend" = function(x) rnorm(x, 0, 1),
  "symmetrical_trend" = function(x) rnorm(x, 0, 0.7),
  "flat_trend" = function(x) rnorm(x, 0, 0.8),
  "sine_trend" = function(x) rnorm(x, 0, 2)
)

N <- c(10, 100, 1000) # size of sequence

# loop through each N and trends
trend_sort_time <- setNames(
  rep(list(setNames(vector("list", length(trend_list)), names(trend_list))), length(N)),
  N)
print(str(trend_sort_time))

## List of 3
##  $ 10  :List of 6
##   ..$ quadratic_trend  : NULL
##   ..$ right_skew_trend : NULL
##   ..$ left_skew_trend  : NULL
##   ..$ symmetrical_trend: NULL
##   ..$ flat_trend       : NULL
##   ..$ sine_trend       : NULL
##  $ 100 :List of 6
##   ..$ quadratic_trend  : NULL
##   ..$ right_skew_trend : NULL
##   ..$ left_skew_trend  : NULL
##   ..$ symmetrical_trend: NULL
##   ..$ flat_trend       : NULL
##   ..$ sine_trend       : NULL
##  $ 1000:List of 6
##   ..$ quadratic_trend  : NULL
##   ..$ right_skew_trend : NULL
##   ..$ left_skew_trend  : NULL
##   ..$ symmetrical_trend: NULL
##   ..$ flat_trend       : NULL
##   ..$ sine_trend       : NULL
## NULL

for (n in N) {
  for (trend in names(trend_list)) {
    trend_sort_time[[as.character(n)]][[trend]] <-
      microbenchmark(
        "bubble_sort" = bubble_sort(Seq),
        "insertion_sort" = insertion_sort(Seq),
        "selection_sort" = selection_sort(Seq),
        "shell_sort" = shell_sort(Seq),
        "merge_sort" = merge_sort(Seq),
        "quick_sort" = quick_sort(Seq),
        times = 100L,
        setup = assign("Seq", 
                       generate_random_sequence(
                         trend=trend_list[[trend]],
                         n=n,noise = noise_list[[trend]]))
      )
  }
}

print(trend_sort_time)

## $`10`
## $`10`$quadratic_trend
## Unit: microseconds
##            expr    min      lq     mean  median      uq     max neval
##     bubble_sort  8.702 10.2505 11.02894 11.1515 11.8010  13.001   100
##  insertion_sort  6.701  7.8000  8.29594  8.2010  8.7510  12.301   100
##  selection_sort 22.600 24.2505 25.36798 25.2010 26.0010  42.802   100
##      shell_sort 41.901 58.4010 69.02209 72.4010 75.6010 108.700   100
##      merge_sort 36.001 37.1005 37.92800 37.5510 38.1010  46.800   100
##      quick_sort 22.701 24.7510 26.13705 25.5010 26.8015  40.601   100
## 
## $`10`$right_skew_trend
## Unit: microseconds
##            expr    min      lq     mean median      uq     max neval
##     bubble_sort 10.301 12.6005 13.19800 13.301 13.8020  16.600   100
##  insertion_sort  6.600  8.4005  8.98492  9.001  9.6010  11.701   100
##  selection_sort 22.601 24.3010 25.72191 25.551 26.3005  38.600   100
##      shell_sort 42.400 59.6505 70.27195 71.900 77.6010 136.601   100
##      merge_sort 35.802 37.7005 39.14108 38.501 39.9010  50.301   100
##      quick_sort 23.302 24.8520 26.92197 26.001 28.6005  40.502   100
## 
## $`10`$left_skew_trend
## Unit: microseconds
##            expr    min      lq     mean  median      uq    max neval
##     bubble_sort  6.801  9.6010 10.50402 10.6010 11.6015 13.401   100
##  insertion_sort  4.800  6.0005  6.61290  6.6000  7.2005  9.501   100
##  selection_sort 22.800 24.3510 25.42905 25.3015 26.1515 39.201   100
##      shell_sort 10.400 29.2015 39.69100 43.5505 46.6015 76.700   100
##      merge_sort 35.502 36.9010 38.19002 37.4510 38.0515 67.802   100
##      quick_sort 22.301 24.0010 25.67712 25.1515 27.1015 35.400   100
## 
## $`10`$symmetrical_trend
## Unit: microseconds
##            expr    min      lq     mean  median      uq    max neval
##     bubble_sort  9.801 11.7015 12.35802 12.4000 13.0010 14.901   100
##  insertion_sort  5.301  6.9510  7.70006  7.7515  8.4015 14.702   100
##  selection_sort 23.000 24.6015 26.00311 25.5520 26.5510 43.901   100
##      shell_sort 11.401 30.7015 43.70806 44.7515 49.7510 90.201   100
##      merge_sort 36.101 37.6010 38.91209 38.3510 39.5515 50.201   100
##      quick_sort 23.401 24.6015 25.96502 25.6010 26.5010 35.201   100
## 
## $`10`$flat_trend
## Unit: microseconds
##            expr    min      lq     mean  median      uq     max neval
##     bubble_sort  8.401 10.9520 11.80194 11.8015 12.8005  14.801   100
##  insertion_sort  4.801  6.8510  7.89802  8.0015  8.7010  12.301   100
##  selection_sort 22.501 24.2010 26.13701 25.3510 26.1510  72.701   100
##      shell_sort 12.001 43.1515 56.74895 58.7505 74.9515 107.101   100
##      merge_sort 36.301 37.3015 38.56210 37.9010 38.8010  52.701   100
##      quick_sort 23.401 24.7010 26.29102 25.6000 27.4510  38.701   100
## 
## $`10`$sine_trend
## Unit: microseconds
##            expr    min      lq     mean median      uq    max neval
##     bubble_sort  9.401 11.3010 11.89404 11.801 12.4515 15.202   100
##  insertion_sort  5.801  7.0010  7.60611  7.502  8.1515 11.401   100
##  selection_sort 22.301 24.3510 25.43092 25.301 26.3010 38.801   100
##      shell_sort 27.201 29.8010 39.04100 41.151 45.0510 70.001   100
##      merge_sort 36.000 37.3000 38.38100 37.901 39.0010 46.802   100
##      quick_sort 22.400 24.6015 26.22907 25.701 27.4515 33.701   100
## 
## 
## $`100`
## $`100`$quadratic_trend
## Unit: microseconds
##            expr     min        lq      mean    median        uq      max neval
##     bubble_sort 755.201  806.5010  842.5420  828.7005  857.1015 1199.201   100
##  insertion_sort 363.601  387.5500  406.8300  399.7010  410.3010  617.902   100
##  selection_sort 344.901  352.6505  367.9370  358.7520  370.6005  534.001   100
##      shell_sort 912.701 1034.2010 1109.3590 1074.8015 1140.0005 1856.201   100
##      merge_sort 474.400  492.5015  522.5970  501.3010  523.5515  813.701   100
##      quick_sort 291.000  309.2010  352.1039  316.0010  325.3510 3277.702   100
## 
## $`100`$right_skew_trend
## Unit: microseconds
##            expr     min        lq      mean    median        uq      max neval
##     bubble_sort 942.002  995.6015 1019.4191 1011.6010 1025.3015 1465.902   100
##  insertion_sort 497.301  529.0515  547.3341  545.8015  560.5515  629.601   100
##  selection_sort 343.700  353.2505  361.6789  357.4510  364.2510  519.501   100
##      shell_sort 978.402 1119.0015 1170.6390 1164.7505 1234.0510 1334.401   100
##      merge_sort 481.101  491.4505  533.5721  501.1515  516.6020 3327.501   100
##      quick_sort 292.501  305.6010  343.5591  313.4515  319.5015 3250.400   100
## 
## $`100`$left_skew_trend
## Unit: microseconds
##            expr     min       lq     mean   median       uq      max neval
##     bubble_sort 652.301 736.7015 752.0631 753.5505 772.5505  909.901   100
##  insertion_sort 217.301 240.3010 250.6229 250.0005 261.6010  295.500   100
##  selection_sort 339.902 351.9015 358.4810 355.1010 362.2010  451.201   100
##      shell_sort 569.101 658.0010 720.6939 717.4010 771.4510  979.801   100
##      merge_sort 471.701 486.3510 517.1070 490.4510 494.8010 3024.701   100
##      quick_sort 286.000 296.4505 305.2390 302.3010 307.0515  388.801   100
## 
## $`100`$symmetrical_trend
## Unit: microseconds
##            expr     min       lq     mean   median       uq      max neval
##     bubble_sort 838.901 874.6505 890.6570 889.6010 905.2010 1014.901   100
##  insertion_sort 354.701 385.6010 398.8620 397.9010 407.9015  490.301   100
##  selection_sort 342.701 351.6015 359.8970 356.8510 363.5015  446.001   100
##      shell_sort 602.400 758.5010 811.2390 820.2510 866.4010 1008.901   100
##      merge_sort 481.100 491.5015 529.3089 500.0505 512.7015 2897.201   100
##      quick_sort 290.101 304.6505 338.6249 310.9005 318.2505 2958.902   100
## 
## $`100`$flat_trend
## Unit: microseconds
##            expr     min       lq     mean   median       uq      max neval
##     bubble_sort 785.802 861.7505 886.5470 882.6010 904.4005 1142.801   100
##  insertion_sort 333.801 383.5510 398.5860 397.1505 412.6005  482.101   100
##  selection_sort 341.400 352.3005 358.1241 356.0515 363.2010  406.401   100
##      shell_sort 796.801 903.7505 960.2370 955.2505 999.8015 1321.401   100
##      merge_sort 487.501 494.8015 558.2080 499.8505 505.3515 3288.301   100
##      quick_sort 288.001 300.4010 308.4991 305.8510 313.2015  388.600   100
## 
## $`100`$sine_trend
## Unit: microseconds
##            expr     min        lq      mean    median        uq      max neval
##     bubble_sort 848.301  894.8005  941.7680  905.9010  922.5010 3580.802   100
##  insertion_sort 391.100  418.0515  429.2330  426.1005  437.7505  522.401   100
##  selection_sort 344.901  353.3505  359.0270  357.5510  363.7015  385.801   100
##      shell_sort 912.601 1020.5015 1091.6780 1086.3515 1148.9015 1462.700   100
##      merge_sort 475.501  490.9515  503.1221  498.4510  511.0510  700.101   100
##      quick_sort 289.001  301.8515  334.6330  307.6515  314.5005 2986.002   100
## 
## 
## $`1000`
## $`1000`$quadratic_trend
## Unit: milliseconds
##            expr       min        lq      mean    median        uq       max
##     bubble_sort 77.121700 79.535302 80.690280 80.324951 81.345401 94.176301
##  insertion_sort 35.157502 36.317000 36.849894 36.797351 37.268451 40.471401
##  selection_sort 28.311901 28.837901 29.545437 29.130201 29.550801 37.026300
##      shell_sort 13.038602 13.704300 14.445973 13.987600 14.695452 18.921400
##      merge_sort  5.885201  6.012301  6.299360  6.077901  6.157651  9.118802
##      quick_sort  3.748401  3.889701  4.493585  3.948901  4.047251 38.053601
##  neval
##    100
##    100
##    100
##    100
##    100
##    100
## 
## $`1000`$right_skew_trend
## Unit: milliseconds
##            expr       min        lq      mean    median        uq      max
##     bubble_sort 94.695301 96.052301 96.885284 96.753602 97.576952 104.7678
##  insertion_sort 49.160101 50.464901 51.123733 51.102101 51.602150  54.7130
##  selection_sort 28.342701 28.751101 29.062010 28.987801 29.222200  31.7264
##      shell_sort 16.557202 17.316050 18.316249 17.703301 19.519852  22.7116
##      merge_sort  5.793101  6.008301  6.516489  6.105751  6.231101  38.0094
##      quick_sort  3.750101  3.868351  4.382523  3.904551  4.016001  10.2119
##  neval
##    100
##    100
##    100
##    100
##    100
##    100
## 
## $`1000`$left_skew_trend
## Unit: milliseconds
##            expr       min        lq      mean    median        uq        max
##     bubble_sort 70.496901 71.935652 74.104811 72.746101 73.915401 138.979800
##  insertion_sort 20.624001 22.191650 22.793862 22.593301 23.284551  26.289601
##  selection_sort 28.436002 29.071300 29.595026 29.373401 29.950151  34.643201
##      shell_sort  9.579702 10.391401 11.266831 10.787351 11.381151  16.650501
##      merge_sort  5.842701  6.059551  6.901749  6.189001  6.550401  37.682601
##      quick_sort  3.691900  3.840301  4.049645  3.900201  4.050451   7.144101
##  neval
##    100
##    100
##    100
##    100
##    100
##    100
## 
## $`1000`$symmetrical_trend
## Unit: milliseconds
##            expr       min        lq      mean    median        uq       max
##     bubble_sort 83.308301 84.818851 85.962545 85.412451 86.097701 98.133102
##  insertion_sort 36.087801 36.869350 37.355421 37.346251 37.695701 39.894001
##  selection_sort 28.867401 29.196051 29.501013 29.388302 29.673751 32.823101
##      shell_sort 13.009501 13.783351 14.718006 14.146551 15.652051 18.485801
##      merge_sort  5.915001  6.094251  6.400552  6.202252  6.380901  9.993301
##      quick_sort  3.799001  3.906701  4.187048  3.972452  4.070252  9.217701
##  neval
##    100
##    100
##    100
##    100
##    100
##    100
## 
## $`1000`$flat_trend
## Unit: milliseconds
##            expr       min        lq      mean    median        uq      max
##     bubble_sort 83.473201 85.648252 88.585357 87.518551 90.483051 104.0141
##  insertion_sort 35.663201 36.900251 38.138400 37.686751 39.067000  43.9789
##  selection_sort 28.709901 29.375252 30.201417 29.824151 30.773100  34.3675
##      shell_sort 13.637201 14.869502 16.221630 15.930850 17.426451  20.6606
##      merge_sort  5.911901  6.174001  6.767467  6.373301  6.723452  23.7372
##      quick_sort  3.778701  3.901002  4.652009  4.095402  4.306351  37.9162
##  neval
##    100
##    100
##    100
##    100
##    100
##    100
## 
## $`1000`$sine_trend
## Unit: milliseconds
##            expr       min        lq      mean    median        uq      max
##     bubble_sort 88.435101 90.336950 92.854573 92.178151 93.836551 105.0604
##  insertion_sort 40.225701 41.665151 42.524901 42.370351 43.116801  46.9237
##  selection_sort 29.121100 30.062351 31.112502 30.991301 31.684151  36.4650
##      shell_sort 14.235902 15.005701 16.936861 16.013751 17.683551  55.9398
##      merge_sort  6.139202  6.331751  6.877558  6.516801  6.923500  13.1538
##      quick_sort  3.888801  4.120852  4.697461  4.275901  4.575251  11.3934
##  neval
##    100
##    100
##    100
##    100
##    100
##    100

Microbenchmark for Special Cases

special_case_sort_time <- setNames(
  rep(list(setNames(vector("list", length(special_case_list)), names(special_case_list))), length(N)),
  N)
print(str(special_case_sort_time))

## List of 3
##  $ 10  :List of 5
##   ..$ already_sorted           : NULL
##   ..$ sorted_backwards         : NULL
##   ..$ one_off                  : NULL
##   ..$ extreme_out_of_place_low : NULL
##   ..$ extreme_out_of_place_high: NULL
##  $ 100 :List of 5
##   ..$ already_sorted           : NULL
##   ..$ sorted_backwards         : NULL
##   ..$ one_off                  : NULL
##   ..$ extreme_out_of_place_low : NULL
##   ..$ extreme_out_of_place_high: NULL
##  $ 1000:List of 5
##   ..$ already_sorted           : NULL
##   ..$ sorted_backwards         : NULL
##   ..$ one_off                  : NULL
##   ..$ extreme_out_of_place_low : NULL
##   ..$ extreme_out_of_place_high: NULL
## NULL

for (n in N) {
  for (sc in names(special_case_list)) {
    special_case_sort_time[[as.character(n)]][[sc]] <-
      microbenchmark(
        "bubble_sort" = bubble_sort(Seq),
        "insertion_sort" = insertion_sort(Seq),
        "selection_sort" = selection_sort(Seq),
        "shell_sort" = shell_sort(Seq),
        "merge_sort" = merge_sort(Seq),
        "quick_sort" = quick_sort(Seq),
        times = 100L,
        setup = assign("Seq", special_case_list[[sc]](n))
      )
  }
}

print(special_case_sort_time)

## $`10`
## $`10`$already_sorted
## Unit: microseconds
##            expr    min      lq     mean  median      uq     max neval
##     bubble_sort  2.600  3.1015  3.97104  3.6010  4.2505  17.202   100
##  insertion_sort  2.400  2.9000  5.41202  3.2010  3.9010 194.302   100
##  selection_sort 23.401 26.2010 35.08290 30.9010 35.7005 112.601   100
##      shell_sort  8.801 10.2010 12.15898 12.1005 13.3510  19.001   100
##      merge_sort 35.301 36.8510 49.45896 47.4005 50.0510 437.901   100
##      quick_sort 23.100 25.5005 31.39705 29.7010 33.4010  87.601   100
## 
## $`10`$sorted_backwards
## Unit: microseconds
##            expr    min     lq     mean  median      uq     max neval
##     bubble_sort 14.600 15.401 17.42304 15.9010 17.8510  79.901   100
##  insertion_sort 12.201 13.201 14.77700 13.9010 16.3505  21.201   100
##  selection_sort 21.701 23.302 26.43298 24.4500 29.7010  47.701   100
##      shell_sort 57.802 60.751 69.13602 62.9510 77.2010 105.501   100
##      merge_sort 36.100 38.251 42.50495 40.3520 45.9005  58.101   100
##      quick_sort 23.902 25.252 28.91710 26.4015 30.5010  80.901   100
## 
## $`10`$one_off
## Unit: microseconds
##            expr    min      lq     mean  median      uq    max neval
##     bubble_sort  4.201  6.2505  8.63302  8.0010 10.9010 17.001   100
##  insertion_sort  2.700  3.8515  5.53097  4.7010  5.7010 46.602   100
##  selection_sort 23.502 25.9010 30.73600 27.5010 32.6000 61.800   100
##      shell_sort  9.601 10.9005 22.29297 12.7015 31.3010 75.601   100
##      merge_sort 34.801 37.1005 41.13604 38.2005 42.3505 87.901   100
##      quick_sort 21.201 25.0010 28.96094 26.6510 31.5005 87.801   100
## 
## $`10`$extreme_out_of_place_low
## Unit: microseconds
##            expr    min      lq     mean  median      uq     max neval
##     bubble_sort  4.801  5.6010  6.44094  6.0505  7.0505  10.401   100
##  insertion_sort  4.501  5.2000  6.69104  5.7010  7.0510  63.502   100
##  selection_sort 22.700 25.0010 30.53505 27.4510 34.7010  57.902   100
##      shell_sort 42.301 44.5015 52.30301 46.3510 59.7510 176.501   100
##      merge_sort 35.801 37.8515 42.69998 39.1510 47.8510  59.900   100
##      quick_sort 23.200 24.9010 28.81597 26.2010 31.7510  60.801   100
## 
## $`10`$extreme_out_of_place_high
## Unit: microseconds
##            expr    min      lq     mean  median      uq    max neval
##     bubble_sort  9.701 10.5010 11.76399 11.0010 12.6515 17.902   100
##  insertion_sort  4.201  4.8005  5.57603  5.0020  5.8510 25.600   100
##  selection_sort 22.301 25.2010 28.54992 26.6010 30.6010 55.601   100
##      shell_sort 26.801 28.8015 33.20297 30.3010 36.9010 57.501   100
##      merge_sort 35.501 36.8515 40.89998 38.2510 44.0515 61.001   100
##      quick_sort 22.201 23.7010 26.35201 24.6005 28.8510 49.201   100
## 
## 
## $`100`
## $`100`$already_sorted
## Unit: microseconds
##            expr     min       lq      mean  median       uq      max neval
##     bubble_sort  15.701  16.8510  19.01006  18.101  20.4505   26.602   100
##  insertion_sort  14.300  16.4510  18.45206  17.901  20.3515   27.600   100
##  selection_sort 378.601 399.5505 437.98806 421.051 467.7010  599.701   100
##      shell_sort 136.801 145.6510 163.63800 153.701 181.4015  234.402   100
##      merge_sort 446.700 477.3010 567.76596 511.851 600.2005 3472.601   100
##      quick_sort 265.201 274.9010 309.18193 290.051 341.0010  480.801   100
## 
## $`100`$sorted_backwards
## Unit: microseconds
##            expr      min       lq      mean    median        uq      max neval
##     bubble_sort 1177.601 1230.551 1343.5760 1296.6510 1437.9505 1777.701   100
##  insertion_sort  776.001  807.201  878.4980  832.5505  947.9010 1157.301   100
##  selection_sort  356.601  371.901  410.8780  395.5010  445.7005  643.901   100
##      shell_sort 1031.801 1076.351 1216.3460 1171.5510 1343.3510 1634.502   100
##      merge_sort  465.501  480.151  610.6300  506.0510  614.1510 4493.800   100
##      quick_sort  314.202  347.251  390.5081  379.1010  429.6010  526.702   100
## 
## $`100`$one_off
## Unit: microseconds
##            expr     min       lq     mean   median      uq      max neval
##     bubble_sort  24.701 191.1010 320.7080 334.5510 459.301  687.601   100
##  insertion_sort  15.201  22.2515  29.5860  28.6500  36.201   52.501   100
##  selection_sort 357.402 381.1010 395.6959 389.2000 403.151  513.800   100
##      shell_sort 138.800 145.9515 181.0031 153.0015 203.251  376.301   100
##      merge_sort 456.200 472.5510 519.1429 484.0010 503.851 2536.601   100
##      quick_sort 232.202 268.2505 278.8930 274.3520 281.151  371.001   100
## 
## $`100`$extreme_out_of_place_low
## Unit: microseconds
##            expr     min       lq      mean   median       uq      max neval
##     bubble_sort  35.502  38.1505  40.83595  39.9010  42.0005   68.302   100
##  insertion_sort  33.600  34.8510  37.21991  36.5505  38.0510   48.500   100
##  selection_sort 356.501 376.8510 393.84712 387.9010 401.2510  493.401   100
##      shell_sort 235.000 241.4510 257.89605 247.2010 265.4515  374.501   100
##      merge_sort 461.900 474.1010 518.92502 482.3010 504.1010 2765.701   100
##      quick_sort 418.401 436.9010 469.91494 460.0015 490.2510  640.800   100
## 
## $`100`$extreme_out_of_place_high
## Unit: microseconds
##            expr     min       lq      mean  median       uq      max neval
##     bubble_sort 544.201 588.8510 614.45002 602.951 632.4015  756.202   100
##  insertion_sort  30.200  32.7005  35.67098  34.500  37.6010   54.101   100
##  selection_sort 371.301 394.2515 424.51198 408.151 440.9000  588.701   100
##      shell_sort 207.301 224.2510 249.17909 237.201 267.7510  386.600   100
##      merge_sort 448.801 479.9505 541.94701 495.551 544.8010 2780.702   100
##      quick_sort 408.301 434.7510 480.76606 471.451 502.9515  725.502   100
## 
## 
## $`1000`
## $`1000`$already_sorted
## Unit: microseconds
##            expr       min         lq       mean     median        uq       max
##     bubble_sort   137.301   147.7010   156.8430   151.9505   164.001   191.600
##  insertion_sort   131.101   139.7505   149.1381   143.8010   152.351   190.001
##  selection_sort 31722.602 32828.1010 33569.0211 33454.4510 34231.851 37283.201
##      shell_sort  2028.500  2161.5010  2370.5590  2228.2510  2346.751  5193.901
##      merge_sort  5295.501  5624.1510  6590.4500  5869.1515  6253.651 48709.601
##      quick_sort  2594.202  2731.4010  3012.5050  2859.0005  3064.702  5698.701
##  neval
##    100
##    100
##    100
##    100
##    100
##    100
## 
## $`1000`$sorted_backwards
## Unit: milliseconds
##            expr        min         lq       mean     median         uq      max
##     bubble_sort 120.753901 126.084951 128.586542 128.826350 131.483401 137.2576
##  insertion_sort  74.881401  79.497750  81.476925  81.002050  83.196001 100.3906
##  selection_sort  31.057801  32.940151  33.777631  33.725052  34.474502  37.5445
##      shell_sort  22.297301  24.122651  26.163534  25.590301  27.725301  35.6588
##      merge_sort   5.627301   6.034701   6.613499   6.298402   6.783251  13.4114
##      quick_sort  13.477501  14.686450  16.499103  15.261800  15.933902  62.2593
##  neval
##    100
##    100
##    100
##    100
##    100
##    100
## 
## $`1000`$one_off
## Unit: microseconds
##            expr       min        lq       mean     median         uq       max
##     bubble_sort   240.701 14448.301 30105.8149 28820.2005 46975.1515 62805.602
##  insertion_sort   139.901   200.251   278.5591   262.0015   335.1505   571.901
##  selection_sort 32559.101 34106.151 34855.4532 34841.3515 35481.2015 42459.401
##      shell_sort  2167.901  2408.301  2679.4590  2593.7005  2809.2010  5386.300
##      merge_sort  5731.302  6216.502  6856.0930  6636.3005  7074.5015 10013.500
##      quick_sort  2778.301  3018.301  3268.6250  3167.4010  3398.6510  6257.900
##  neval
##    100
##    100
##    100
##    100
##    100
##    100
## 
## $`1000`$extreme_out_of_place_low
## Unit: microseconds
##            expr       min         lq       mean    median        uq       max
##     bubble_sort   341.701   363.5510   399.9689   388.601   437.101   506.200
##  insertion_sort   322.500   336.1005   367.8799   348.351   401.151   485.700
##  selection_sort 31566.600 34015.5000 34891.1699 34807.751 35527.050 40731.801
##      shell_sort  2473.101  2618.6010  2942.9130  2838.901  3061.401  5681.901
##      merge_sort  5567.802  6184.1510  6934.9599  6635.450  7289.201 10077.201
##      quick_sort 25652.501 27203.9005 28210.4190 28154.101 28903.150 37087.702
##  neval
##    100
##    100
##    100
##    100
##    100
##    100
## 
## $`1000`$extreme_out_of_place_high
## Unit: microseconds
##            expr       min         lq       mean    median         uq       max
##     bubble_sort 53595.401 57278.4010 58927.5870 58949.151 60415.5015 65525.201
##  insertion_sort   288.300   301.0515   336.8219   313.700   361.3515   956.601
##  selection_sort 32668.901 34605.2005 35648.7830 35609.201 36666.5505 40146.600
##      shell_sort  2428.901  2549.2010  2827.1720  2690.552  2919.1505  5244.700
##      merge_sort  5542.401  6020.1510  6750.0020  6540.651  7141.4510 13988.701
##      quick_sort 23654.902 25506.0010 26494.3230 26285.052 27463.2505 32669.501
##  neval
##    100
##    100
##    100
##    100
##    100
##    100

It’s not easy to detect any obvious trend with only numbers, so in the next post, I’ll try to find ways to visualize these results to make differences more apparent.

coding

Sorting Comparison

Write Sorting Algorithms

Generate Unordered Sequences with Varying Trends

Sorting with Different Algorithms

See also